Exkurze do třídírny nekonečen je zcela vyčerpávající, přestože není obsahově vyčerpávající. Průměrnému technicky vzdělanému jedinci by ke spokojenosti mělo stačit poznání, že v zásadě existují nekonečna dvě (alespoň co se týče kardinálních čísel): jedno je menší, říkáme mu spočetné, a jedno větší, tomu říkáme nespočetné. To první si spočítáte na prstech (pokud máte zajištěn neomezený přísun rukou), zatímco to druhé nikoliv.
Jak porovnávat nekonečna
Porovnávání nekonečných množin sice není tak jednoduché jako třeba porovnávání výše výplaty, ale dá se udělat na podobném principu. Představte si, že sedíte s měšcem plným zlaťáků ve středověké hospodě, neumíte vůbec počítat, a přesto byste rádi věděli, zda vám toho v měšci cinká víc než tomu zarostlému pacholkovi, co sedí naproti vám a co chvíli vám prská do žejdlíku piva.
I když nemáte ani páru o vyšší matematice a nějaké sčítání vám nic neříká, můžete si při porovnání finančního obsahu obou měšců vypomoci následujícím trikem. Vylovíte ze svého měšce zlaťák, prásknete s ním vítězoslavně o hrubou desku stolu a vyzvete pacholka odnaproti, aby vaše gesto zopakoval se svým měšcem. Pacholek tedy dorovná svojí mincí. Pak prásknete s druhým zlaťákem a pacholka požádáte o totéž. Pak s třetím, čtvrtým a tak dále. No a komu dojdou zlaťáky dřív, ten má v měšci míň peněz. A pokud vám ty zlaťáky náhodou dojdou současně, jinými slovy pokud se pacholkovi podařilo na každý zlaťák z vašeho měšce kontrovat jeho vlastním zlaťákem, ale ani o chlup víc, tak máte přesně stejně peněz.
Dvě nekonečné množiny se porovnávají zrovínka takovým způsobem. Vysolíte na stůl prvky jedné množiny, a pokud pro každý její prvek najdete prvek té druhé množiny, kterým můžete zakontrovat, zlaťák za zlaťák, tak máte dvě úplně stejně velké množiny, byť třeba nekonečné.
Jinými slovy, pokud se nám podaří prvky obou množin přesně spárovat, tak mají stejný počet prvků (odborně říkáme, že mají stejnou mohutnost). U nekonečných množin musíte samozřejmě vymyslet nějaký abstraktní mechanismus (třeba algoritmus nebo formulku), jak to spárování provést, jinak hrozí, že budete v té knajpě sedět u stolu až do alelujá. Z logiky spárování musí také vyplynout, že se obě množiny tímto procesem vyčerpají – jinými slovy, že ani v jednom měšci nezůstanou žádné zlaťáky.
Jde vlastně o stejný princip, jako když jsme v jednom z předchozích Matykání dávali dohromady tanečníky a tanečnice (technicky se tomu spárování říká vzájemně jednoznačné zobrazení).
Spočetné nekonečno
Nejjednodušší verze nekonečna existuje v podobě přirozených čísel, tedy 1, 2, 3, 4, 5, 6, 7, ... Tato čísla současně reprezentují jakýsi zlatý standard pro ostatní nekonečné množiny. Všechny množiny, které mají – ve smyslu předchozí sekce – stejný počet prvků jako přirozená čísla, se označují jako spočetné. Spočetná množina je tedy taková, jejíž prvky (tanečníci) se dají přesně spárovat s přirozenými čísly (tanečnicemi). Nebo trochu jinak: prvky spočetné množiny se dají označit (onálepkovat) přirozenými čísly – jako když si na poště taháte lístky s čísly, která vám říkají, kdy na vás přijde řada.
Dříve než se podíváme na pár spočetných množin, rozmyslete si následující odstavec.
Pokud vám nějaký lapka odstraní z měšce polovinu zlaťáků, tak je jasné, že máte najednou méně peněz než před okradením. Polovina vašich zlaťáků se rozhodně nedá spárovat s jejich původním množstvím. U nekonečných množin to bohužel neplatí a občas se může stát, že „polovina“ vaší množiny bude stejně veliká jako množina původní (opět ve smyslu předchozí sekce). Takže selský rozum si raději odložte v šatně.
Nejjednodušším příkladem tohoto paradoxu jsou sudá čísla. Na první pohled se zdá, že sudých čísel je o polovinu méně než přirozených čísel. Nicméně z modrého panelu níže na obrázku vidíme celkem jasně, že pro každého (černého) sudého tanečníka si lehce najdeme (červenou) tanečnici z množiny přirozených čísel (prostě to sudé číslo vydělíme dvěma) a toto spárování obě množiny přesně vyčerpá. Jsou tedy podle předchozí sekce stejně velké (mají stejnou mohutnost).
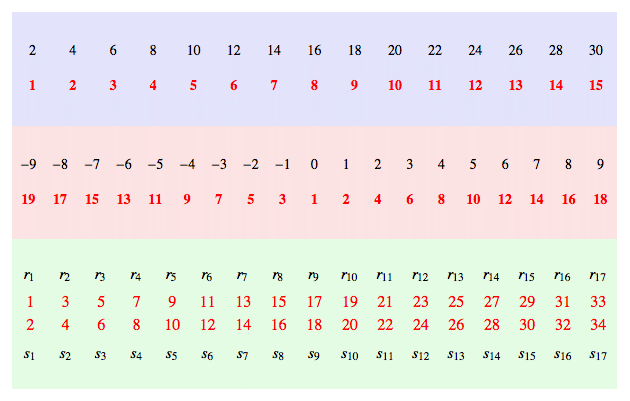
Na prostředním (červeném) panelu vidíte podobný argument pro celá čísla
(v černém). Těch se pro změnu zdá být více (protože obsahují i 0 a záporná čísla), ale není tomu tak. I tady si červené tanečnice
přirozených čísel své tanečníky najdou, ale musí to udělat chytře. Ta
první si zatančí s nulou (proto je pod černou 0 červená
1) a pak holky při výběru tanečníků
skáčou střídavě doprava a doleva. Tady si samozřejmě musíte představit,
že tanečníci pokračují až do nekonečna jak vpravo, tak vlevo. Nicméně
nakonec se obě množiny přesně vyčerpají a ani jeden tanečník a ani jedna
tanečnice nám nepřebývá. Takže i celých čísel je spočetně.
Z posledního (zeleného) panelu si můžeme odnést trochu abstraktnější poznatek – pokud sesypeme dohromady dvě spočetné množiny (jejich prvky jsem označil písmenky r a s), dostaneme opět spočetnou množinu, protože červené tanečnice přirozených čísel si prostě vybírají své tanečníky na přeskáčku.
Podstatně více vrásek nám nadělají zlomky. Těch už je skutečně hodně. Odborně říkáme, že je jich „jako psů“, tedy hafo. Když si kladné zlomky napíšete do tabulky tak, že v prvním sloupci máte „jedniny“, ve druhém „poloviny“, ve třetím „třetiny“ atd. (viz obrázek), tak se zdá, že zlomků je nekonečně mnoho nekonečen, tedy zdánlivě víc než spočetně – každý sloupek sám o sobě je totiž nekonečný (ve směru dolů) a máme jich nekonečně mnoho (ve směru doprava).
I tady si však mazané červené tanečnice poradí, ovšem teď už musejí být „prefíkané ako líšky“. Při výběru tanečníků se vydají podél žluté cestičky a berou si je na parket v tom pořadí, jak je potkávají. A začnou vlevo nahoře. Takže první bude tančit s 1/1, druhá s 1/2, třetí s 2/1, čtvrtá s 3/1, pátá s 2/2, šestá s 1/3, sedmá s 1/4, osmá s 2/3, devátá s 3/2 a tak dále. V této části už jsem červená čísílka raději nemaloval, aby z toho nevznikl grafický guláš, rozmyslete si ale, že touto klikatou cestou se skutečně dostanete ke každému zlomku a spárování tudíž proběhne bez potíží. Pro šťouraly dodávám, že zlomky, které nejsou v základním tvaru (třeba 2/4), můžete během párování přeskočit.

Je doufám jasné, že se zápornými zlomky můžeme zatočit úplně stejně,
takže jak záporné, tak kladné zlomky představují spočetnou množinu. Z výše uvedeného zeleného panelu navíc víme, že když sesypeme dvě
spočetné množiny dohromady, vznikne opět spočetná množina. Takže všech
zlomků je stejně tolik co přirozených čísel, tedy „jen“
spočetně mnoho, přestože to tak ze začátku nevypadalo.
Nespočetné nekonečno
Mohlo by se zdát, že všechny nekonečné množiny jsou spočetné a to, jak se dají spárovat s přirozenými čísly, závisí pouze na „fikanosti“ tanečnic. Ale není tomu tak. Už Georg Cantor, jeden ze zakladatelů moderní teorie množin, ukázal, že když si vezmeme číselnou osu (tedy množinu čísel reálných či lidověji desetinných), tak její prvky (desetinná čísla) s přirozenými čísly spárovat nelze. Ono dokonce nelze spárovat ani opticky menší množinu: jednotkový interval (0,1), tedy všechna desetinná čísla mezi 0 a 1.
Georg Cantor si všiml, že ať spárování sesmolíme jakkoliv, vždycky se nám podaří najít desetinné číslo, které ve výsledném seznamu není. Jinými slovy, ať jsou ty holky fikané, jak chtějí, minimálně na jednoho tanečníka se nedostane tanečnice.
Nejjednodušším způsobem, jak spárování realizovat, je sestavit si tabulku desetinných čísel, ve které bude každý řádek odpovídat jednomu přirozenému číslu (desetinná čísla níže jsem vybral náhodně, ale pro jakýkoliv jiný výběr proběhne argumentace úplně stejně).
1) 0,634825741...
2) 0,017563369...
3) 0,896044321...
4) 0,812023987...
5) 0,740032871...
6) 0,343866709...
7) 0,190454382...
8) 0,878731338...
9) 0,563260451…
...
(a tabulka samozřejmě pokračuje až do nekonečna)
...
Takže jednička tančí s 0,634825741, dvojka s 0,017563369, trojka s 0,896044321 atd.
Pojďme se teď podívat, jak nezadaného tanečníka (tedy desetinné číslo, které se do seznamu nedostalo) objevit. Základním nástrojem k nalezení tohoto „chybějícího“ čísla je skutečnost, že k tomu, aby se dvě desetinná čísla lišila, stačí, když se budou lišit v jedné jediné číslici (třeba 0,428351... je jiné číslo než 0,428451…, protože se liší ve zvýrazněné číslici).
Pokud tedy chceme sestrojit číslo, které v naší tabulce není (tj. které se liší od každého čísla v tabulce uvedeného), stačí to narafičit tak, aby se od každého čísla v tabulce lišilo pouze jednou jedinou číslicí. Konkrétně to uděláme tak, že se od prvního čísla bude lišit v první číslici, od druhého čísla v druhé číslici, od třetího ve třetí a tak dále.
Za tím účelem jsem u prvního čísla tučně zvýraznil první číslici, u druhého druhou atd.
A teď už to bude celkem brnkačka: změníme (jakkoliv!) všechny zvýrazněné číslice a z nich vytvoříme kýžené číslo č. Například pokud v tabulce zmenšíme všechny zvýrazněné číslice o jedničku (a z 0 uděláme 9), dostaneme následující číslo:
č = 0.505925220...
Toto desetinné číslo v našem seznamu evidentně není, protože se liší alespoň jednou číslicí od každého čísla na seznamu. Na každém řádku jsme si totiž jednu číslici půjčili (tu tučně zvýrazněnou) a tu jsme při konstrukci čísla č změnili. Chachá, hloupí vlci. A i když si to spárování uděláte jinak, chybějící číslo č tímto způsobem vždycky najdete.
Takže desetinných čísel mezi 0 a 1 je sice nekonečně mnoho (rozmyslete si proč), ale není to nekonečno spočetné. Nedá se spárovat s přirozenými čísly – jako třeba zlomky. Je to nekonečno úplně jiného typu: říkáme mu nespočetné. A dokud jsme v ráži, tak si hned ukážeme, že i všech desetinných čísel – jak asi tušíte – je nespočetně mnoho.
Abychom viděli, že jednotkový interval a celá číselná osa mají stejnou mohutnost (stejný počet prvků), musíme se opět vrátit k myšlence první sekce a najít si vhodné spárování tanečních partnerů, ovšem s tím rozdílem, že tanečnice (červené) tentokrát nebudou přirozená čísla, ale desetinná čísla z intervalu (0,1) a tanečníci (ti modří) budou vybráni z celé číselné osy. Spárování se dá odvodit graficky z posunuté funkce ArcTan – viz obrázek.

Provedeme to takto. Pro každou červenou tanečnici (tedy číslo mezi 0 a 1 na
ose y) vystřelíme vodorovně raketu a tam, kde raketa narazí na graf naší
funkce, tak se stočí svisle dolů a vybere jednoho modrého tanečníka na
číselné ose (osa x). Z obrázku je jasné, že dvě různé tanečnice budou
mít vždy dva různé tanečníky a naopak. Nikdo nezůstane sedět.
Z této konstrukce tedy vyplývá, že na celé číselné ose je přesně tolik bodíků, co v relativně malém intervalu (0,1). A to i přesto, že interval je součástí číselné osy. V obou případech je bodíků nespočetně mnoho. Já jsem vás varoval, že jste si měli selský rozum odložit v šatně.
Takže sečteno a podtrženo máme víceméně dvě nekonečna. Menší, spočetné, které si můžete představit jako přirozená čísla, a nebo cokoliv, co se s nimi dá spárovat – třeba zlomky. Můžete se na něj dívat jako na diskrétní typ nekonečna. Pak je tu setsakramentsky velké nekonečno nespočetné: například počet všech bodů v jednotkovém intervalu a nebo cokoliv, co se s ním dá spárovat (například celá číselná osa, ale taky třeba jednotkový čtverec!). Někdy se tomuto nespočetnému nekonečnu říká kontinuum, protože má v podstatě spojitý charakter.
Pokud vás toto téma zajímá a umíte anglicky, doporučuji přečíst si následující kapitoly o spočetných a nespočetných množinách (autor: Jerry Farlow). Tam se mimochodem dozvíte i to, jak to zaonačit s jednotkovým čtvercem (jak jeho bodíky spárovat s bodíky v jednotkovém intervalu, kterých je zdánlivě méně, protože živoří na jeho hraně). Pokud vás ještě nebolí hlava, tak si rozvažte, že tento čtverec je vlastně tvořen nespočetně mnoha jednotkovými úsečkami – pro každou souřadnici y (a těch je nespočetně mnoho) máte jednu. Přesto se tyto na první pohled nesouměřitelné množiny (tedy přesněji jejich body) dají spárovat.
Hypotéza kontinua
Georg Cantor tohle všechno věděl už někdy koncem 19. století. Jedné bezesné noci ho však napadlo, zda náhodou neexistuje ještě nějaký jiný typ nekonečna – něco mezi tím spočetným a nespočetným. Tedy zda by se na číselné ose nedala najít množina, která je (co do mohutnosti) více než spočetná, ale méně než nespočetná.
Cantor se domníval, že taková množina existovat nemůže a že každá množina, která má více prvků než spočetná, už nutně musí být nespočetná. Dokonce svým kolegům kolem roku 1882 napsal, že bude mít důkaz během několika týdnů. Ale jak se do věci zamotával, důkaz se mu jevil stále obtížnější a obtížnější, až nakonec musel kapitulovat a jeho stále nedokázanému tvrzení se začalo říkat hypotéza kontinua.
Ani zbytek vědeckého světa si však s touto zapeklitostí nevěděl rady a hypotéza kontinua se postupem času stávala slavným matematickým problémem. O její prestiži svědčí i to, že ji David Hilbert v roce 1900 zařadil na první místo v seznamu nevyřešených problémů tehdejší matematiky.
Nakonec se to všechno vyvrbilo celkem šalamounsky. Kurt Gödel v roce 1940 ukázal, že se hypotéza kontinua v rámci standardní teorie množin (Zermelo Fraenkel) nedá vyvrátit, a v roce 1963 na něj navázal Paul Cohen zjištěním, že v rámci téže teorie se nedá ani dokázat. Hypotéza kontinua je tedy v podstatě na stávající teorii množin nezávislá. Abychom ji dokázali (nebo vyvrátili), budeme potřebovat lepší a úplnější teorii množin. Takovou ale zatím nemáme.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




