Jedním z obávaných strašáků vyšší matematiky je tzv. epsilon-delta definice limity. S trochou nadsázky bychom mohli říct, že na Matfyzu slouží jako síto, kterým se oddělují chlapci od mužů. Tak si na tu příšeru trochu posvítíme.
Svět se mění. Již Herakleitos pravil „Panta Rei“ (vše plyne), a tudíž je nemožno vstoupit se starými Řeky dvakrát do téže řeky. Lidé jsou ale tvorové zvídaví, chtějí hned všechno měřit, a proto se brzy začali pídit, jak rychle se ten náš svět vezdejší vlastně vyvíjí.
Pokud nás zajímá rychlost změny dané veličiny v průběhu nějaké doby, řekněme od času T do času T', pak to není problém. To, co se vyvíjí, popíšeme nějakou funkcí f(t), která nám říká, jaký je stav veličiny v čase t (ať už je to dráha ujetá vozidlem či objem vody v děravém zásobníku). No a pak prostě vydělíme změnu veličiny změnou času a dostaneme fundamentální vztah pro (průměrnou) rychlost této změny:
RZ = (f(T) - f(T')) / (T - T')
Někdy nás ale nezajímá průměrná rychlost za předchozí hodinu, ale momentální rychlost teď a tady. To znamená, jak rychle se veličina mění právě v tomto okamžiku. Zafixujeme si tedy T a zkusíme najít co nejmenší hodnotu T' > T, pro kterou se výše uvedený podíl dá vyčíslit. V tom je ale malý háček.
My bychom v podstatě potřebovali si za T' zvolit nejbližší číslo vpravo od T. To ale není žádná legrace. Zatímco třeba vojáci mají při nástupu útvaru vždy nejbližšího souseda po pravé ruce (a blíž už zaručeně nikdo nestojí), pro reálná čísla se takový nejbližší soused hledá obtížně.
Ale právě nebližší soused po pravé ruce má pro výpočet momentální rychlosti změny klíčový význam. Proto jeho nalezení věnovali matematici značné úsilí, a to nejprve intuitivně, pomocí tzv. infinitesimálů, tedy nekonečně malých veličin, a později o něco přesněji pomocí pojmu limita.
Právě limita se stala základním kamenem partie matematiky, která má studium změn v popisu práce, tedy diferenciálního počtu (v zahraničí též zvaného Calculus).
Málem bychom skončili s infinitesimálem
Celá diferenciální habaďůra je založena na celkem jednoduchém pozorování. Čtverec z malého čísla je podstatně menší než číslo samotné. A čím je číslo menší, tím je jeho čtverec (relativně vzato) zanedbatelnější. Stačí se podívat na pár příkladů:
0.12 = 0.01
0.012 = 0.0001
0.0012 = 0.000001
0.00012 = 0.00000001
Proto se při počítání s velmi malými čísly dají všechny vyšší mocniny prakticky zanedbat. A speciálně to platí pro čísla nekonečně malá, tzv. infinitesimály. Jejich teorie je docela zajímavá a má za sebou poměrně klikatý vývoj od původně intuitivních pojmů až po různá zobecnění reálných čísel.
Básníci si mohou infinitesimál vyrobit svépomocí podle vzoru „stanu se menším a ještě menším, až budu prvním infinitesimálem na tomto světě“.
Podívejme se, jak tahle vymyšlenost zhruba funguje.
Vezměme si běžnou kvadratickou funkci
f(x) = x2
a zeptejme se, jak rychle se v nějakém bodě x mění.
Infinitesimál si označím písmenkem h a budeme si ho představovat jako úplně malilinkaté (ale nenulové) čísílko – v absolutní hodnotě menší než jakékoliv kladné reálné číslo. Výraz x + h je tedy v jistém smyslu tím „dalším vojákem vpravo“, kterého jsme v úvodu hledali. Posuneme se od hodnoty x „o fous“ doprava a podíváme se, jak to zacloumalo s funkční hodnotou.
Okamžitá změna kvadratické funkce f(x) v bodě x bude dána výrazem
(f(x + h) - f(x)) / h = ((x + h) 2 - x2)/h = (2xh + h2) / h
a protože jsme si řekli, že u malilinkatých čísel (a h takové je) se dají naprosto zanedbat všechny jejich vyšší mocniny, člen h2 s klidným svědomím zanedbáme a dostaneme pro rychlost změny známý výraz
RZ = 2xh / h = 2x
který samozřejmě v moderní matematice známe pod heslem „derivace x2 je 2x“ (tj. v bodě řekněme x = 3 je rychlost změny kvadratické funkce rovna RZ = 2x = 6).
To znamená, že pokud se z bodu x = 3 posuneme doprava o nějakou malou změnu dx, pak se hodnota funkce zvýší o dy = 6 dx. Tj. s každým zvýšením x o nějakou jednotku, se y zvýší o 6 jednotek. To je praktický význam „rychlosti změny“.
Samozřejmě musíme mít na paměti, že rychlost změny se mění s proměnnou x – jakmile se z bodu x pohneme doprava, řekněme do bodu x' = 3.1, pak musíme rychlost změny přepočítat (RZ = 6.2). Pokud bychom si tedy chtěli funkci „zrekonstruovat“ pouze ze znalosti funkční hodnoty f(3) = 9 a ze znalosti rychlosti změny, museli bychom náš propočet RZ neustále kontinuálně aktualizovat. Tím se zabývají diferenciální rovnice, na které se mrkneme časem.
Povšimněte si závěrem, že v konečném výrazu pro RZ už žádný infinitesimál není. Nemá tam co dělat, okamžitá rychlost změny závisí pouze na funkci a bodu x. Ten infinitesimál je pouze něco jako první stupeň rakety – splní svou funkci a odhodí se. Proto nás nemusí moc trápit, že jsme ho výše definovali tak lajdácky.
Limita, konečně je odlita
V jistém smyslu se na limitu dané funkce v daném bodě skutečně můžeme dívat jako na zobecnění pojmu „nejbližšího vojáka stojícího po pravé (či levé) ruce“.
Koneckonců, celá čísla takový pojem znají. Vezměme si třeba n = 37. To číslo má dva přirozené sousedy. Po pravé ruce stojí n + 1 = 38 a po levé n – 1 = 36.
Pro čísla reálná ale žádný přirozený pojem sousedních čísel neexistuje. Limita funkce f v bodu c nám ho v jistém smyslu nahradí (pro lepší notaci viz obrázek dole).
L = lim{x --> c}f(x)
Je to číslo L, ke kterému se blíží funkční hodnoty y, pokud se hodnoty argumentu x blíží k c. Samozřejmě v drtivé většině případů je to číslo L prostě funkční hodnota f(c). Nejzajímavější limity jsou proto v případech, kdy je v bodě c nějaký problém – obvykle nespojitost funkce.
Doporučuji vzít si kalkulačku a nějaký seznam limit a chvilku si s tím hrát. Tedy dosazovat do dané funkce hodnoty blížící se c (ale ne rovné c) a koukat se, co se děje s funkční hodnotou. Dva tři experimenty „na vlastní pěst“ toho prozradí víc než stránka popsaná formulkami.
A protože limitní chování zleva i zprava se může lišit, rozlišujeme limitu zprava a limitu zleva. Pouze v případě, že jsou obě stejné, budeme mluvit o limitě. Podívejme se teď na ně vizuálně. Nebude to úplně přesný obrázek – a někdo z matematiků mi za to nejspíš umyje hlavu – ale v první aproximaci se to snese.
Na dalším obrázku je vykreslená funkce f(x) = x2 / x, která je definovaná pro všechna reálná čísla s výjimkou nuly (tou dělit nesmíme). Pro nenulová čísla je funkce pochopitelně totožná s funkcí g(x) = x (proto je její graf přímkou). Aby to nebylo nule líto, dodefinujeme v ní naši funkci libovolně třeba předpisem
f(0) = 1
A to ještě není všechno. Uděláme takový malý matematický zločin a představíme si, že graf funkce se sestává z diskrétní posloupnosti bodíků (jako by byl vygenerován počítačem – což on koneckonců je).
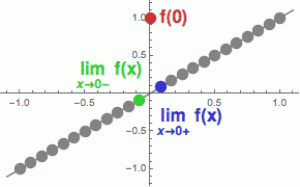
Ten červený bodík (resp. jeho y-souřadnice) je funkční hodnota, zelený bod je limitou v nule zleva (značí se 0-, jako že se tam blížíme ze záporna) a modrý bod je limita v nule zprava (značí se 0+, jako že se tam blížíme z kladna, a ne třeba ze Slaného). Obě limity – zprava i zleva – nám vlastně naznačují, co se s funkcí děje v nejbližším okolí bodu c = 0.
Nebo jinak: pokud z grafu funkce vyjmete bod c, vzniknou na něm dvě visuté plošiny (oddělené tou dírou po bodu c). Limity ukazují, kde jsou hraniční y-hodnoty těch plošin.
Speciálně bych zdůraznil, že limita v daném bodě (ani zprava ani zleva) nemusí mít nic společného s funkční hodnotou v tomto bodě. Funkce dokonce nemusí být v bodě ani definována, a přesto v něm může mít limitu (což by byl případ naší funkce, kdybychom ji na poslední chvíli v nule nedodefinovali). Pokud je funkční hodnota i obě limity jedno a to samé číslo, pak říkáme, že funkce je v bodě x spojitá (to znamená, že její chování v bodě c je úzce spjato s chováním „těsně“ napravo i nalevo, tedy lidově že funkce nemá v bodě c skok či nějakou anomálii).
Teď si možná řeknete – počkat, ale kdybychom si místo té naší funkce vzali funkci f(x) = x (která je v nule definovaná a má tam hodnotu f(0) = 0), tak tam se tři obarvené kuličky sobě pořád nebudou rovnat (ta zelená bude trochu níž než červená a modrá naopak).
Tady ta kuličková analogie trochu selhává, protože na obrázku jsem je vykreslil s určitým konečným poloměrem (a v určité vzdálenosti od sebe). Ve skutečnosti je nutno si jak poloměr, tak vzdálenost představovat bodově, tj. libovolně malou (infinitesimální). Takže v případě funkce f(x) = x by ty tři kuličky měly skutečně stejnou hodnotu 0 (na ose y).
Analogie s vojáky, kterou se nám podařilo s kuličkami trochu nakamuflovat, ale nefunguje ještě v jednom důležitém ohledu. Pro celá čísla pravý a levý soused vždy existují. U reálných čísel to nemusí být pravda.
Podívejme se třeba na funkci Q(x), která je definována takto. Q(x) = 0 pro racionální čísla a Q(x) = 1 pro iracionální (graf je schematicky znázorněn vlevo, kde jsem všechny hodnoty Q(x) = 1 vyznačil tenkou úsečkou, aby vynikla jejich hustota). Tady vůbec není jasné, kde by zelená a modrá kulička měly být umístěny (červená bude v nule, protože 0 je racionální číslo, takže Q(0) = 0). V libovolné blízkosti bodu x = 0 se totiž vyskytují jak racionální, tak iracionální čísla a žádné z nich není to „nejbližší“. Jak se blížíme s hodnotou x k 0 (ať zprava či zleva) tak funkční hodnoty f(x) divoce přeskakují mezi 0 a 1.
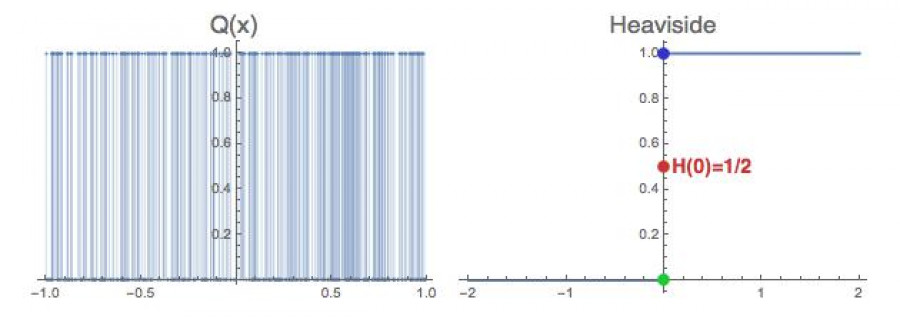
Zkrátka ona ta limita v sobě nenese ani tak informaci o chování funkce v tom „nejbližším bodu“ (který notabene neexistuje), jako spíš informaci o chování funkce v bezprostředním okolí daného bodu. Pojem limity je založen na tom, že funkční hodnoty se něčemu (modré či zelené kuličce) blíží. A pokud je to blížení příliš divoké, tak limita holt neexistuje. V pravé části obrázku je naopak tzv. Heavisideova funkce, která má v nule hodnotu 1/2, limitu zleva 0 a limitu zprava 1.
Abychom tyto úvahy mohli postavit na nějaký solidnější základ, podívejme se na klasickou definici limity. Ta se s pojmem „bezprostředního okolí bodu c“ (což je termín trochu „na vodě“) popasovala tak, že jeho šířku nastavila pružně podle potřeby přesnosti na ose y.
Tento „klouzavý“ pojem bezprostředního okolí bodu c je odpověď Calculusu na potřebu mít definován pojem sousedního bodu vpravo a vlevo.
Epsilon delta gymnastika, oko z toho trochu tiká
Začneme s limitou v nekonečnu, což je v jistém smyslu nejpřirozenější možná limita. V nekonečnu samozřejmě žádná funkce definována není, takže limita je pro nás jedinou možností, co naše funkce tam někde daleko „u nekonečna“ vlastně vyvádí (znalci tvrdí, že nekonečno je podstatně dál než Austrálie).
V jednom starším Matykání jsme sledovali posloupnosti bodů a dohodli jsme se, že posloupnost xn bude mít v nekonečnu limitu L (xn --> L), pokud každé okolí bodu L v sobě obsahuje všechny členy posloupnosti od určitého indexu výše. Taková posloupnost je v podstatě zobrazení z množiny indexů do množiny reálných čísel, a protože ta limita je v nekonečnu (n = ∞), dá se v podstatě říci, že všechny body posloupnosti, jejichž indexy jsou nekonečnu dostatečně blízko, se zobrazují do okolí hodnoty L.
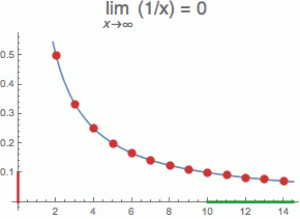
Ještě lépe je to vidět, pokud si posloupností proložíme funkci. Například místo posloupnosti 1/n (červené bodíky) budeme uvažovat modrou funkci f(x) = 1/x. Intuitivně je jasné, že když s x kráčíme do nekonečna, tak se y hodnoty přibližují k nule. Nula je tedy limitou funkce v nekonečnu. Ale jak to postihnout?
V podstatě to znamená, že od určitého x výše (zelený interval na ose x) jsou všechny funkční hodnoty dostatečně malé neboli všechny funkční hodnoty leží dostatečně blízko nule (v červeném intervalu na ose y).
A pokud červené okolí trochu smrskneme (aby to pro červené bodíky bylo obtížnější), tak prostě to zelené posuneme trochu doprava, aby se funkční hodnoty do toho smrsknutého okolí vešly. A to je princip fungující v definici limity.
Jen to zkusíme přeformulovat topologicky (tj. místo žonglování s pojmem „vzdálenost“ budeme žonglovat s pojmem „okolí“). Červený interval je okolím nuly (resp. jeho součástí), zatímco na zelený interval se můžeme dívat jako na okolí nekonečna. Důležitý rozdíl spočívá v tom, že okolí konečných bodů smrskáváme tak, že stahujeme délku příslušného intervalu, zatímco okolí nekonečna smrskáváme tak, že zelený interval posouváme doprava (tj. uvažujeme větší a větší čísla). S délkou intervalu tady operovat nemůžeme, protože k nekonečnu je to vždycky nekonečně daleko (tj. intervaly by měly nekonečnou délku). Je to trochu zvláštní náhled, ale vyplatí se nám.
Pro limitu v nekonečnu, říkejme jí L, teď můžeme vystřihnout definici takto: pro každé předem zvolené okolí hodnoty L (na ose y) se dá najít „okolí nekonečna“ (na ose x) tak, že všechny hodnoty x z tohoto okolí se zobrazují na y hodnoty v onom předem zvoleném okolí hodnoty L.
A z toho ušijeme definici limity pro libovolný bod c (tentokrát konečný). Funkce f(x) má v bodě c limitu L, pokud pro každé okolí hodnoty L (na ose y) existuje okolí bodu c (na ose x), jehož všechny body se zobrazují do zmíněného okolí L. Pokud mluvíme o limitě jednostranné, uvažujeme pouze okolí pravá či levá.
Prakticky se ta okolí pochopitelně definují pomocí nerovností. Např. pravé okolí bodu c (o šířce δ) je množina hodnot x splňujících:
0 < x - c < δ
pro oboustranné okolí stejné šířky budeme potřebovat absolutní hodnotu
0 < |x - c| < δ
Ukažme si to na limitě zprava: Funkce f(x) má v bodě c (zde je c = 0) limitu zprava, říkejme jí L (viz obrázek vlevo), pokud pro každé okolí hodnoty L (jehož šířka je tradičně značena písmenkem ε) lze najít pravé okolí bodu c (jehož šířka je stejně tradičně značena δ), tak že funkce f zobrazuje to pravé zelené δ okolí (bodu nula) na ose x kompletně do červeného ε okolí (bodu L) na ose y.
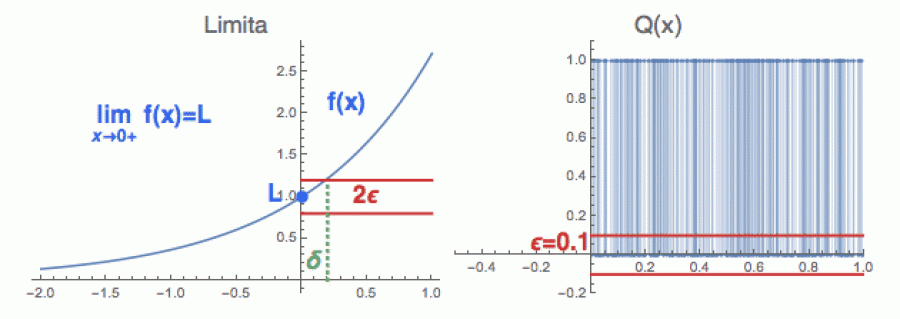
Geometricky se pro každé ε okolí δ najde pomocí té tečkované čáry. Pokud to ε trochu zmenšíte, tak se geometricky lehce upraví i hodnota δ (taky se musí příslušně zmenšit). Obdobně by se to udělalo pro limity zleva – i když tam by to δ obecně vyšlo trochu jinak (naše funkce není symetrická kolem nuly). Pro limitu oboustrannou by se pak muselo vzít menší z obou δ, aby se funkční hodnoty vešly do červeného pásu jak vlevo, tak vpravo.
Algebraicky by se musely vyřešit příslušné nerovnice (což je podstatou důkazu existence limit). Geometrie nám slouží pouze jako vodítko pro přemýšlení. Tu skutečnou práci obstarává algebra.
V pravé části obrázku je opět skákavá funkce Q(x). U ní vidíte, že pro malá ε (např. ε = .1) už se žádné pravé δ-okolí, které by se kompletně zobrazovalo do ε-okolí na ose y, najít nedá. Iracionální body z něho vždy vyskočí do jedničky.
Tady byste mohli namítnout, že pro hodně velké ε (řekněme ε = 10) by se δ-okolí najít dalo (a limita by tudíž existovala), protože z tak širokého ε−okolí by se v rámci této funkce vyskočit prostě nedalo. Ale taková definice limity by nám nebyla k ničemu (byla by příliš benevolentní). Proto je v definici limity napsáno nekompromisně „pro každé okolí“ (a to se týká hlavně těch setsakramentsky malých). To, že se v definici zajímáme hlavně o libovolně malá ε-okolí, de facto supluje ty infinitesimály. Čím je ε-okolí menší, tím je i δ-okolí (které se do něho zobrazuje) přiměřeně menší a zkoumáním jejich vzájemných proporcí de facto testujeme chování funkce v infinitesimálním okolí bodu c. Proto se při modelování infinitesimálu nesmíme upnout na jednu konkrétní hodnotu ε, ale musíme ho popsat pomocí jakési relace mezi ε a δ.
A jak se definice zapíše rigorózně matematicky? Používají se v ní logické kvantifikátory:
∃ ... existuje (např. ∃x, tak že x > 0...)
∀ ... pro každé (např. ∀n přirozené se dá najít prvočíselný
rozklad)
S nimi můžeme definici (oboustranné) limity lim f(x) = L zapsat jako:
∀ε>0 ∃δ>0 tak, že kdykoliv je |x - c| < δ pak je |f(x) - L| < ε
a pro srovnání i pro posloupnost: xn --> x0
∀ε > 0 ∃n0 > 0 tak že pro všechna n > n0 je |xn - x0| < ε
Všimněte si, že první podmínka definuje okolí c (respektive indexu posloupnosti), zatímco ta druhá říká, jak se má chovat y (respektive člen posloupnosti). Pro limity zleva či zprava se pak nerovnosti jen přizpůsobí intervalům, ve kterých se snažíme lokální chování funkce popsat.
De facto jsme tak pojem „nejbližšího bodu po pravé ruce“ nahradili pojmem „nejbližšího intervalu po pravé ruce“ a vhodným žonglováním s tímto pojmem jsme ten infinitesimál nahradili. Namísto zkoumání podílu infinitesimálů (jako v první sekci) zkoumáme chování miniaturních okolíček a díky nim jsme schopni postihnout i to nejlokálnější chování funkce v okolí daného bodu.
A teď konkrétně, spojitě i diskrétně
V jednom starším Matykání jsme viděli, že celou matematikou se táhne pevninský zlom mezi diskrétním a spojitým popisem světa. A zasahuje i do limit.
Posloupnosti jsou diskrétními objekty, zatímco funkce náleží do světa spojitého. V obou světech lze definovat limitu v nekonečnu, což je taková pramáti všech limit. Ta existuje pouze zleva (pro plus nekonečno), či zprava (pro minus nekonečno), protože na druhé straně nekonečna nic není. Tedy přesněji řečeno je tam jedna velká jáma, kam se vozí hrubky z písemných úloh studentů gymnázia.
Spojité a diskrétní světy se pochopitelně do jisté míry prolínají. Například v definici spojitosti se lze odkázat přímo na limitu funkce a odvodit z ní epsilon-delta verzi, ale také je možné se odvolat na diskrétní limity posloupností a definovat spojitost funkcí pomocí nich.
Spojitost je v našem vesmíru naprosto fundamentální pojem, bez kterého by se kvantitativní analýza prakticky nedala dělat. Představte si ten chaos, kdyby si funkce mohly dělat, co chtějí. Mezi jejich hodnotami by neexistovala žádná souvztažnost. Jen díky spojitosti jsme schopni předpovědět hrubý tvar funkce na nějakém okolí pouze ze znalosti funkční hodnoty v daném bodě a nějakých těch derivací (což jsou v podstatě indikátory růstu). Spojitost zaručí, že funkce neodskočí někam úplně jinam a derivace nám obvykle prozradí, kterým směrem se funkční hodnoty vydaly – což je základem jejich analýzy.
Styčných ploch mezi oběma světy je povícero. V úvodu jsme viděli, že třeba limitu funkce 1/x v nekonečnu si lze dokázat zhruba pomocí stejných triků jako limitu posloupnosti 1/n.
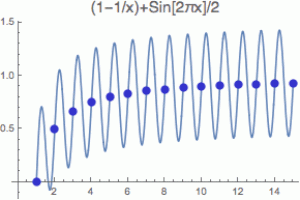
Přesto musíme být opatrní, protože matematici jsou vždy schopni nám předhodit nějaký špek. Vezměme si třeba funkci:
f(x) = (1 – 1 / x) + sin(2 * π * x) / 2
Pokud ji vyčíslíme pouze v celých číslech, dostaneme posloupnost (modré body), která zjevně konverguje k 1 (tj. lim f(n) = 1), zatímco lim f(x) v nekonečnu neexistuje, protože funkce jako taková si mezi modrými bodíky neustále osciluje a nemá se k tomu, aby se k nějaké hodnotě začala přibližovat.
Pro tuto situaci se pak používají různé vychytávky jako limsup a liminf, které v podstatě sledují, co se děje s maximy a minimy, když se blížíte k nekonečnu. Ale s tím si nebudeme lámat hlavu.
A jak se limity počítají? Buď se na ně používají algebraické triky (podobně jako když jsme výše počítali ten kvadratický infinitesimál), anebo se odvodí kombinací z limit, které lze (někdy poměrně pracně) odvodit z definice.
Mezi nejznámější limity pro h --> 0 patří exponenciála
lim (exp(h) - 1) / h = 1 (důkaz zde)
a sinus
lim sin(h) / h = 1 (důkaz zde)
Z těchto dvou limit (a těch algebraických) si pak nasekáte prakticky všechny ostatní.
Spočítejme si například limitu funkce sin(x) / x2 v nule zprava. Naše funkce se dá rozepsat na součin dvou faktorů: (sin(x) / x) * (1 / x). První faktor se pro malé kladné hodnoty blíží 1, zatímco druhý nekonečnu, takže jejich součin bude nekonečno. A to je hledaná limita.
A co třeba limita v nule zprava funkce ln(1 + x) / x. Poučeni předchozím příkladem, můžeme si funkci rozepsat jako ln(1 + x) * (1 / x). První výraz se v nule zprava blíží k nule, druhý k nekonečnu. A nula krát nekonečno je tzv. neurčitý výraz (může nabývat libovolné hodnoty), který nemůžeme prostě jen tak pronásobit jako nahoře. Nula si prostě na nekonečnu vyláme zuby.
Zkusme tedy limitu převést na exponenciálu substitucí 1 + x = exp(y). Tj. všechna x zaměníme na y podle substitučního vztahu. Tím se naše funkce přemění na y / (exp(y) - 1). Když si v substitučním vztahu dosadíte za x nulu, vyjde vám, že y musí být také nula (tj. limita pro x blížící se k nule bude limitou pro y blížící se také nule – tady to dokonce platí oboustranně). A limita v nule pro funkci y / (exp(y) - 1) už je reciproká hodnota výrazu, který se blíží jedničce (to byla první z limit nahoře). A protože reciproká hodnota 1 je 1, limita původně uvažované funkce ln(1 + x) / x bude také jedna.
Jakmile máme limity v malíčku, můžeme se vrátit k původnímu problému výpočtu rychlosti změn (RZ) v bodě c a místo přehazování infinitesimálů vidlemi je vyjádřit pomocí limity (pro h --> 0)
RZ = lim (f(x + h) - f(x)) / h
A to je v podstatě začátek diferenciálního počtu.
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




